Women's Worlds, Ottawa, July 7, 2011 Download a PDF

The base number of Western culture is ONE: One god, one life, one soul. Consequently, Western cultures use linear math and a linear exchange economy. However, Native American cultures use a base number of TWO and, as a result, developed binary math. Our binary concepts are shorthanded in the woodlands as Blood and Breath; west of the Mississippi, as Water and Air. Same thing.

Next is where Westerners get really lost: Since our whole unit necessarily consists of two equal parts, what looks like ONE to Europeans looks like ONE-HALF to us. Therefore, each half must have a complementary half to make it truly ONE—at which point, it requires a companion to make our requisite Two.

Thus, the Direction of the Sky consists of Two halves: East (1/2) and West (1/2). Put the two halves together, and suddenly we have the One Direction of the Sky, which, itself becomes One-half in need of its complement, the Split  Sky, or North (1/2) and South (1/2). Only when the Direction of the Sky is complemented by the Split Sky, do we have One Whole. The directions may look like Four to Westerners, but, to us, they look like One balanced set.

This thinking winds up in our “plus sign” motif so common in Native American jewelry. The most authentic of these motifs doubles the plussign, showing that it is a binary, as in Figure 1., a beaded pouch. Just to keep life interesting, we also tilt the plus sign  into an X, so that it is the in-betweens, not the lines, that matter. We are all about middles. When everything is a middling, nothing can be an outlier.

Translating all of this into a gift economy must make room for complex human interaction, besides, which is where fractals come into gifting. Fractals represent continual, self-replicating action, which is the modus operandi of the gift economy.

Figure 1. Blackfeet Beaded Pouch

Figure 1. Typical Beaded Pouch, showing version of "plus sign". http://www.native-languages.org/bags.htm.

Fractals are the same pattern, repeating endlessly, writ small, writ large, and writ everything in between. As far as Westerners know, the term "fractal" was coined in 1975 by Benoît Mandelbrot, and then refined as The Fractal Geometry of Nature in 1982.¹ This might have been the first that Westerners had heard of fractals, but that does not mean that no one else had thought of, or more to the point, used fractals prior to Mandelbrot.

In fact, Asians and Native Americans had been well aware of fractal thinking since forever. In Figure 1, the famous painting, "Great Wave off Kanagawa," the first print of thirty-six in the series, "Views of Mount Fuji," by the Japanese artist, Hokusai (1760-1849) clearly demonstrated the concept of fractals in nature, long before Mandelbrot. Tiny fractal repetitions of waves on the larger wave crests replicate the macro-wave.

Mandelbrot's fractals were not binary, but Native American fractals are. In fact, our plus sign symbol is fractal. Depictions of fractals like this are limited, in that they have measured and static replications, but the basic idea comes across. Natural fractals, such as the gift, are not measured.

The next image, Figure 2., below, is a plus sign rotated into an X, with the fractal repetitions mimicking chaos in nearly seventy groups. The same image repeats in various sizes, which is not a bad representation of the interaction of the Iroquois League at its over sixty member states, by the late eighteenth century. Important to Native American concepts is the balance that this binary fractal embodies.

Figure 1. "Great Wave off Kanagawa"

Figure 1., "SOURCE: I am indebted to "Mathematical Paintings and Sculptures," posted 12 July 2009 and accessed 17 March 2010, for picking up on this example of fractals in action. .

Figure 3. is even better, because in this binary X fractal, the overall effect looks haphazard, more closely replicating the action of gift-giving than the previous visual. In this one, although the large gifts are the most obvious at first, a closer look shows that the whole is actually held up by the infinity of small, even miniscule, fractal gifts.

Figure 2. A Binary Fractal

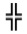Figure 2. A Binary Fractal. Notice the plus sign rotated into an X, with the fractal repetitions mimicking chaos. This image is courtesy of Mark Dow

Figure 3. The Binary Fractal of the Gift Economy

Figure 3. The Binary Fractal of the Gift Economy. Again, the halves are twinned, with the actions, small and large, endlessly replicated. The colors here are capricious, as supplied by their creator, Mark Dow, and harbor no deep meaning. This image is courtesy of Mark Dow

Gift economies include such binary fractals but are much harder to depict on a screen than static fractals, because gift economies are:

1. multiple
2. internally multi-dimensional
3. constant motion

Thus, groups of binary fractals interact with one another in perpetual motion.

http://wn.com/Moving_Fractals

(First video, only; 14 seconds)

Once the gift economy is in motion, it can be very strong, because it has no, one central nervous system. Thus, 500 years of the attempted murder of our gift economies have done damage, but they have not yet stopped the motion of the smallest parts, which are the building blocks of the whole.

I think it is important for discussions of gift economies to recognize that they consist of complex, fractal binaries. Such thinking requires a paradigm shift: the linear math of the exchange economy simply cannot explain the binary movement of fractal economics.

¹Benoît Mandelbrot, Les objets fractals, forme, hasard et dimension (1975); in English as Fractals: Form, Chance and Dimension (San Francisco: W. H. Freeman and Co, 1977); Benoît Mandelbrot, The Fractal Geometry of Nature (San Francisco: W. H. Freeman & Co, 1982).